You can create a number of line drawings by starting with a simple pattern that is recursively subdivided in parts, each of which is (at least approximately) a reduced-size copy of the whole. The results are related to mathematical objects called “fractals”, and so images generated in this manner are often called "fractal" images.
One example of a fractal curves is the “Koch curve” introduced by Swedish mathematician Helge von Koch in 1904. You can derive a Koch curve by beginning with the following basic four-segment piece:
You then replace each line segment of the diagram with a smaller copy of itself.
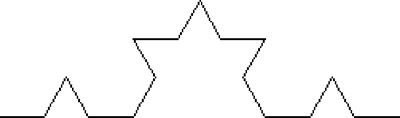
You again replace each line segment of the diagram with a smaller copy of the basic shape.
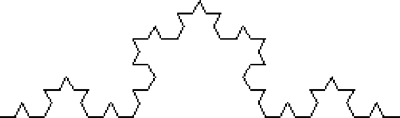
Koch curves display an intricate beauty, as the number of levels of replacement increases. An even more remarkable figure can be created by joining three Koch curves as if they were the sides of a triangle. This figure is often referred to as a "Koch snowflake":

The procedure for creating a Koch curve is usually recursive. At each level, we observe that a Koch curve is made up of four smaller Koch curves. This process can be described in the following pseudocode:
if level < 1 then
Move forward length pixels
else
Draw a k-1 level Koch curve with segments 1/3 the current length
Turn left 60 degrees
Draw a k-1 level Koch curve with segments 1/3 the current length
Turn right 120 degrees
Draw a k-1 level Koch curve with segments 1/3 the current length
Turn left 60 degrees
Draw a k-1 level Koch curve with segments 1/3 the current length
- Write a KochCurve program that uses DrawingTool and provides a drawKochCurve method for drawing Koch curves. Each drawKochCurve method can take the number of levels and an initial size as its parameters. Sample usage of the method to draw a 6 level Koch curve of length 300 would be:
KochCurve curve = new KochCurve();
curve.drawKochCurve(6, 300);
Create a Koch Snowflake. The Koch snowflake includes three Koch curves arranged in a triangle.
- Turn in your source code and run outputs.


