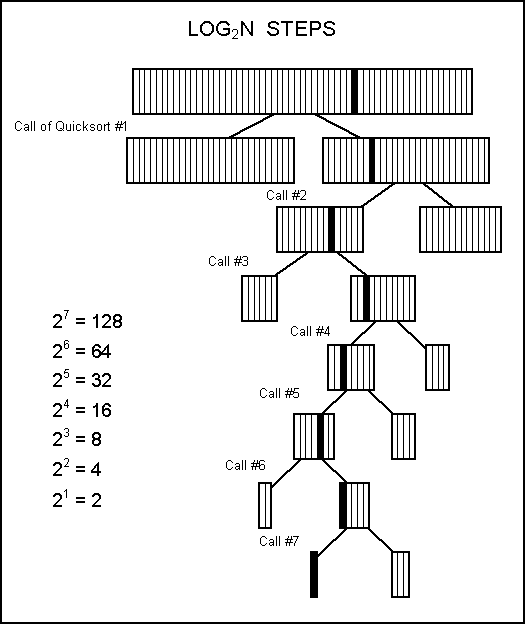
Determining the order of QuickSort, O (N* log₂N), is a difficult process. The best way to understand it is to imagine a hypothetical situation in which each call of quickSort results in sublists of the same size. Let’s try a size of 128, because it is a power of 2.

If a list has 128 elements, the number of calls of quickSort required to move a value into its correct spot is log₂128, which equals 7 steps. Dividing the list in half gives us the log₂N aspect of QuickSort.

But we need to do this to 128 numbers, so the approximate number of steps to sort 128 numbers will be 128 * log₂128. A general expression of the order of QuickSort will be O(N * log₂N). An O(N * log₂N) algorithm is a more specific designation of the broader category called O(N * log N).

A graph of an O(N* log₂N) algorithm is close to a linear algorithm, for large values of N. The log₂N number of steps grows very slowly, making QuickSort a dramatic improvement over the O(N²) sorts.